Monday, September 30, 2019
Friday, September 27, 2019
Wordy Puzzle
Word problems have always been a bit confusing for me and this one took me a while to think about. Since the words were confusing, I drew a picture to try to understand what is happening.
Who is speaking?
I am speaking.
Who is "that man"?
That man is my son.
What makes this difficult/interesting?
This was difficult for me because there were no numbers. It was all words and we do not know who is speaking. The play on English words and usage of father adds to the confusion. It is interesting because one has to use logic and problem solving in a different way to figure out who is speaking and to determine that "that man's father" = "my father's son".
Math Art Reflection
After browsing the works on Bridges website, our group really liked Yvette's piece the best. It was visually interesting and also had mathematical concepts involved. I think my group did an amazing job by bringing more math into art by having set rules and systems (some with math history elements as well). It will be a good way to get students who are strong in art or learn well by creating to get a better understanding of some concepts. Furthermore, it will help all students to visualize what is happening with irrational/rational numbers and visually see the difference.
Although we did not get to do this for our presentation, we had discussed using different textures to represent a digit or even incorporating braille in order to make this activity accessible for students who have visual impairments. It is definitely worth while to use a project like this in the classroom to get students to work together.
Monday, September 16, 2019
The Locker Problem
After reading this problem, I tried to visualize it. Since it is not reasonable for me to visualize 1000 lockers at once, I decided to start by looking at only the first 10 lockers. After drawing it out and summarizing the findings, I tried to find a pattern. So far, the perfect squares less than 10 remain closed. I would try to test this by observing the next 10 lockers to see if this pattern holds. If it does, then the lockers that would remain closed would be {1,4,9,16}.
Letters From Past Students
Student 1:
I really enjoyed your class. You helped me understand math that was useful not only in class but in life. I felt like I mattered in your class even though I struggled with some of the math concepts. Thank you for always being there to listen to me and taking our thoughts and feelings into consideration when teaching.
Student 2:
Your class was the worst. It was boring and irrelevant and a waste of my time. You made no sense and math is more confusing now. I don't remember anything from your class and I never needed to use anything. I didn't feel like I belonged in your class or that I could do math.
My Thoughts:
I hope to create a classroom environment where students feel safe enough to talk to me about what they don't understand and how I can help them learn better, a place where they are not afraid of making mistakes and can learn with each other. Although it would be wonderful if everyone came out of my class loving math, I would be much happier if my students left feeling competent to handle challenges that came to them. I worry that I will fail in trying to create this environment or in my attempts to entice students into trying new things in math since many are used to a very basic approach.
I really enjoyed your class. You helped me understand math that was useful not only in class but in life. I felt like I mattered in your class even though I struggled with some of the math concepts. Thank you for always being there to listen to me and taking our thoughts and feelings into consideration when teaching.
Student 2:
Your class was the worst. It was boring and irrelevant and a waste of my time. You made no sense and math is more confusing now. I don't remember anything from your class and I never needed to use anything. I didn't feel like I belonged in your class or that I could do math.
My Thoughts:
I hope to create a classroom environment where students feel safe enough to talk to me about what they don't understand and how I can help them learn better, a place where they are not afraid of making mistakes and can learn with each other. Although it would be wonderful if everyone came out of my class loving math, I would be much happier if my students left feeling competent to handle challenges that came to them. I worry that I will fail in trying to create this environment or in my attempts to entice students into trying new things in math since many are used to a very basic approach.
Math & Me
-Ross and Rachel type of relationship
-I couldn't remember which way the 5 went in kindergarden but forced myself to learn by not looking at the number line hanging by the doorway
-Hated math in grade 5 because I did not understand how to long divide but was helped by my dad and that "ah ha" moment was wonderful and I went back to loving math
-Grade 8 and 9 math was meh but it got very interesting in grade 10. My teacher was fantastic and there was a lot of overlap and connections to other subjects which made it more magical to learn (slopes in physics etc.)
-Grade 10 math made me want to learn more and pursue mathematics which is what I did
-I specifically wanted to teach because I went from hating to loving math because I had people in my life who helped me get the "ah ha" moments and I wanted to be one of those people for someone else
-It is very rewarding being able to help someone understand something they found so confusing
-I couldn't remember which way the 5 went in kindergarden but forced myself to learn by not looking at the number line hanging by the doorway
-Hated math in grade 5 because I did not understand how to long divide but was helped by my dad and that "ah ha" moment was wonderful and I went back to loving math
-Grade 8 and 9 math was meh but it got very interesting in grade 10. My teacher was fantastic and there was a lot of overlap and connections to other subjects which made it more magical to learn (slopes in physics etc.)
-Grade 10 math made me want to learn more and pursue mathematics which is what I did
-I specifically wanted to teach because I went from hating to loving math because I had people in my life who helped me get the "ah ha" moments and I wanted to be one of those people for someone else
-It is very rewarding being able to help someone understand something they found so confusing
Saturday, September 14, 2019
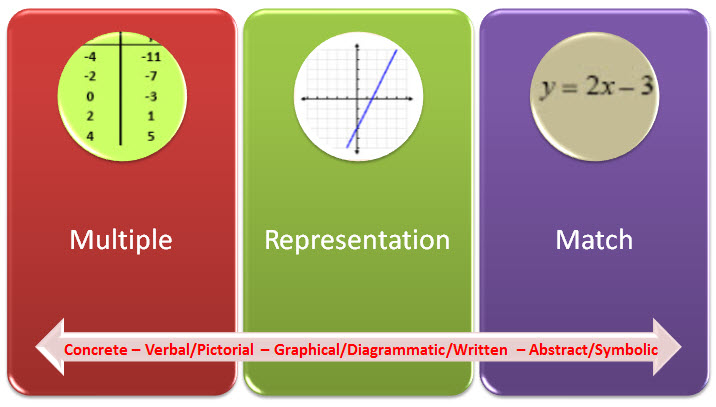
Mathematical Understanding & Multiple Representations
What convinces (or doesn't convince) you in the authors' argument?
I do believe students learn better when exposed to different techniques since they will be more flexible. It also opens up learning to students who learn better by visual/graphical processes which makes concepts accessible to other types of learners. That being said, I appreciated that the author used some visuals in his article to help make some of the points/examples clear. I would have benefited from some more examples and explicit definitions.
If we are viewing it as a process rather than an end product we should provide the students with the materials during an assessment. I think the author assumes that all students are able to connect the external and internal abstractions quickly and easily. Since we know that all students are different and have different strengths, they should all be allowed to have the materials that can help them succeed.
What kinds of mathematical representations are included and excluded in this article? Can you think of an example of a mathematical representation of a particular math concept (from secondary or elementary school curricula) that is not included, but that might be helpful for students in developing understanding? Describe briefly how you might teach using this representation.
The article did not include technology based representations. If the school has access to a 3D printer students will be able to explore 3 dimensional shapes and can get a better understanding of surface area and volume by figuring out how much material is needed to create a hollow vs solid shape.
It also did not mention using students as a representation. Recalling my history of mathematics course, I remember one group created a video where they performed proofs via dance. I think this is a great way to get students to physically understand what is happening since they are physically performing it themselves.
Furthermore, as mentioned in class, this type of physical movement could be used to graph parabolas and other types of graphs to get the roots and understand the shape and what is going on in the graph. They can examine the roots, areas of increase/decrease etc.
I do believe students learn better when exposed to different techniques since they will be more flexible. It also opens up learning to students who learn better by visual/graphical processes which makes concepts accessible to other types of learners. That being said, I appreciated that the author used some visuals in his article to help make some of the points/examples clear. I would have benefited from some more examples and explicit definitions.
If we are viewing it as a process rather than an end product we should provide the students with the materials during an assessment. I think the author assumes that all students are able to connect the external and internal abstractions quickly and easily. Since we know that all students are different and have different strengths, they should all be allowed to have the materials that can help them succeed.
What kinds of mathematical representations are included and excluded in this article? Can you think of an example of a mathematical representation of a particular math concept (from secondary or elementary school curricula) that is not included, but that might be helpful for students in developing understanding? Describe briefly how you might teach using this representation.
The article did not include technology based representations. If the school has access to a 3D printer students will be able to explore 3 dimensional shapes and can get a better understanding of surface area and volume by figuring out how much material is needed to create a hollow vs solid shape.
It also did not mention using students as a representation. Recalling my history of mathematics course, I remember one group created a video where they performed proofs via dance. I think this is a great way to get students to physically understand what is happening since they are physically performing it themselves.
Furthermore, as mentioned in class, this type of physical movement could be used to graph parabolas and other types of graphs to get the roots and understand the shape and what is going on in the graph. They can examine the roots, areas of increase/decrease etc.
Tuesday, September 10, 2019
Relational Understanding vs. Instramental Understanding
Three things that made you "stop" as you read this piece, and why
1. "By many, probably a majority, his attempts to convince them that being able to use the rule is not enough will not be well received."
Is this really true? Multiple times I have heard students question why what they're learning is relevent and when they would be able to use it. Clearly these students are wanting a deeper understanding. Furthermore, when students realize that the rule they learned isn't working anymore or if the context of the problem is changed, they will be confused and not know what to do or they will get the question wrong.
2. "Over-burdened syllabi. Part of the trouble here is the high concentration of the information content of mathematics."
Although having a dense curriculum would make it difficult to go deeper into a topic and spend enough time to have relational understanding, I don't think it is completely to blame. If students have a firm grasp of the early concepts in early years, they will be confident in them going into the next year and can build upon them. I wonder if it would be easier for students to learn a topic in a year than move on to a new topic the next year. This way teachers could focus on one topic and build upon it at their own pace without having to do lots of recap to help the students remember the previous material.
3. "Difficulty of assessment of whether a person understands relationally or instrumentally."
I found it very interesting how Skemp proposes that mathematics students are examined orally. It would be beneficial for the students who find it difficult to get their thoughts on paper and are more comfortable with vocalizing the steps they are doing. I think this should be an option for those students who have an understanding of math but are unable to effectively communicate that understanding via pencil and paper. In order to have a record of the assessment, I would keep a recording of the conversation so that I could have something to reference. It would also be useful to the student to reflect back on their assessment.
Where you stand on the issue Skemp raises, and why
I believe students should be taught relationally initially. However, I am not opposed students learning and using "the rules" once they have relationally understood the concept. It is irresponsible mathematics to give students a formula/trick for particular problems without offering an explanation of why it works. Once students have a grasp on the concept, I don't see a problem with them using some short cuts or rules. Since mathematics is constantly building on prior concepts, it is to the students benefit to be comfortable with prior concepts. Furthermore, being able to complete certain problems quickly (such as factoring polynomials) will help the students focus on the new material being presented. I do think it would be beneficial to revisit the old material briefly before moving onto the new material so that the students could see the connection.
1. "By many, probably a majority, his attempts to convince them that being able to use the rule is not enough will not be well received."
Is this really true? Multiple times I have heard students question why what they're learning is relevent and when they would be able to use it. Clearly these students are wanting a deeper understanding. Furthermore, when students realize that the rule they learned isn't working anymore or if the context of the problem is changed, they will be confused and not know what to do or they will get the question wrong.
2. "Over-burdened syllabi. Part of the trouble here is the high concentration of the information content of mathematics."
Although having a dense curriculum would make it difficult to go deeper into a topic and spend enough time to have relational understanding, I don't think it is completely to blame. If students have a firm grasp of the early concepts in early years, they will be confident in them going into the next year and can build upon them. I wonder if it would be easier for students to learn a topic in a year than move on to a new topic the next year. This way teachers could focus on one topic and build upon it at their own pace without having to do lots of recap to help the students remember the previous material.
3. "Difficulty of assessment of whether a person understands relationally or instrumentally."
I found it very interesting how Skemp proposes that mathematics students are examined orally. It would be beneficial for the students who find it difficult to get their thoughts on paper and are more comfortable with vocalizing the steps they are doing. I think this should be an option for those students who have an understanding of math but are unable to effectively communicate that understanding via pencil and paper. In order to have a record of the assessment, I would keep a recording of the conversation so that I could have something to reference. It would also be useful to the student to reflect back on their assessment.
Where you stand on the issue Skemp raises, and why
I believe students should be taught relationally initially. However, I am not opposed students learning and using "the rules" once they have relationally understood the concept. It is irresponsible mathematics to give students a formula/trick for particular problems without offering an explanation of why it works. Once students have a grasp on the concept, I don't see a problem with them using some short cuts or rules. Since mathematics is constantly building on prior concepts, it is to the students benefit to be comfortable with prior concepts. Furthermore, being able to complete certain problems quickly (such as factoring polynomials) will help the students focus on the new material being presented. I do think it would be beneficial to revisit the old material briefly before moving onto the new material so that the students could see the connection.
Wednesday, September 4, 2019
Subscribe to:
Comments (Atom)